最小生成树

最小生成树

什么是最小生成树呢？对于一个有n个点的图，我们显然知道其边数大于等于n-1，那么假如说我们选n-1条边，使其连接所有的n个点，并且这些边的权值和最小，那么这n-1条边所形成的树就叫做最小生成树

求最小生成树有两个经典算法：Prim算法和Kruskal算法，其中Prim算法有朴素版和堆优化版。对于稀疏图我们可以用朴素的Prim算法和Kruskal算法，对于稠密图我们可以用堆优化的Prim算法

Prim算法

和dijkstra算法类似，我们先找到不在集合当中的距离最小的点t，然后用t去更新其他点到目标点的距离（运用了松弛定理），然后把t加入集合中（集合存放的是已经确定了最短距离的点）

Prim算法几乎是一模一样的思路：

  • 初始化距离为正无穷
  • 迭代n次，每一次找不在集合当中的距离最小的点，赋值给t，用t更新其他点到集合的距离（注意更新的是到集合的距离，这也是和dijkstra算法的唯一不同之处），然后把t加入到集合当中去。

这里到集合的距离的定义是点到集合内部的所有边当中长度最小的边

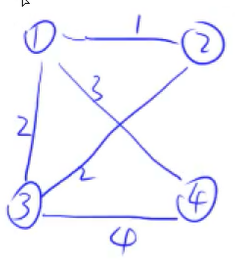
我们以一个简单的图为例子：

ppWTKlq.png

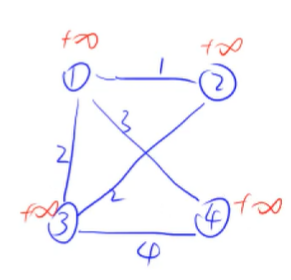
然后我们初始化距离：

ppWT1mT.png

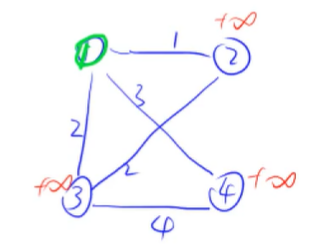
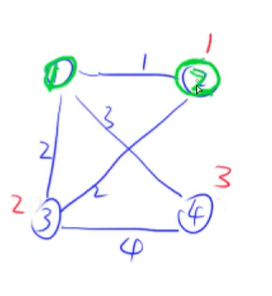
然后我们选择1号点，进行迭代（在集合中的点标记为绿颜色）：

ppWTUpR.png

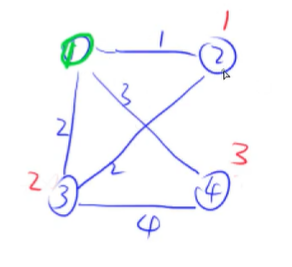
用这个点更新一下其他点的距离（用红色表示）：

ppWTd6x.png

这样我们就完成了第一次迭代，接下来我们选择一个不在集合中的距离最近的点（也就是2号点），来进行第二次迭代：

ppWTr7D.png

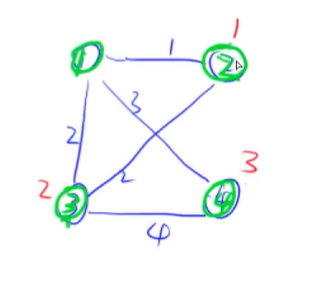
然后不断的迭代，这里略去中间的步骤了，最后得到的结果如下图：

ppWT6tH.png

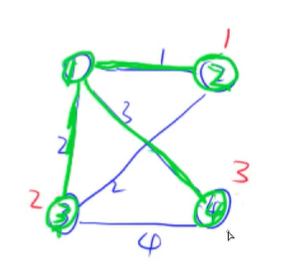
那么我们的最小生成树是什么呢？其实我们不难发现，我们找到的最短路就是最小生成树的一条边，我们把得到的最短路画出来，得到一个树：

ppWTWct.png

这就是我们要得到的最小生成树，这个算法就是Prim算法

这里有几个问题需要注意一下：

  • ①为什么要迭代n次而不是像dijkstra算法一样迭代n-1次？dijkstra算法寻找的是最短路，最后一个点肯定是最短的了不需要讨论了（迭代也无法更新最小距离），而prim算法求的是到集合的距离，最后一个点到集合的距离不一定是最小的，因此需要额外讨论一次
  • 能否对负边权使用？答案是可以的，这也是和dijkstra算法不同的地方。我们回顾一下dijkstra算法的松弛定理，无非就是一条更新语句d[j]=min(d[t]+g[t][j],d[j])，显然这个松弛操作只对正边权具有单调性，对于负边权不具有单调性，因此不能用于负边权问题；而prim算法中的更新语句并不用松弛定理，因为d数组的含义是到集合的距离，我们只需要单纯的比较就可以了，d[j]=min(d[j],g[t][j])，这对于负边权是适用的

事实上，在所有最小生成树的算法中，都可以考虑负边权

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
using namespace std;
const int N = 510,INF = 0x3f3f3f3f;

int n,m;
int g[N][N];
int dist[N];
bool st[N];

int prim()
{
    //初始化最小距离
    memset(dist,0x3f,sizeof(dist));
    int res = 0;
    for(int i=0;i<n;i++)
    {
        int t = -1;//假如是第一个点，则就不用比较直接更新距离最小点
        //得到不在集合中的距离最小点
        for(int j=1;j<=n;j++)
            if(!st[j] && (t == -1 || dist[j] < dist[t]))
                t = j;
        //假如不为第一个点并且最小距离为INF，说明这个点不连通任何一个点，那么没有最小生成树
        if(i && dist[t] == INF) return INF;
        //先更新res
        if(i) res+=dist[t];
        //更新其他点的最小距离
        for(int j=1;j<=n;j++) dist[j] = min(dist[j],g[t][j]);
        //把当前点加入集合
        st[t] = true;
    }
    return res;
}

int main()
{
    cin >> n >> m;
    memset(g,0x3f,sizeof(g));
    while(m--)
    {
        int a,b,c;
        cin >> a >> b >> c;
        //重边无向图的处理方式
        g[a][b] = g[b][a] = min(g[a][b],c);
    }
    int t = prim();
    if(t == INF) cout << "impossible";
    else cout << t;
    return 0;
}

Kruskal算法

Kruskal算法的算法流程非常简单：

  • 将所有边按权重从小到大排序（可以选择快排，即sort），这一步是整个算法流程中最慢的一步（我们称其为决速步），时间复杂度为O(mlogm)O(mlogm)，但是常数非常小，这是排序算法的特性
  • 枚举每条边a–b，权重为c，如果两点不连通，把a–b这条边加入集合中

至此我们就结束了Kruskal算法，整个算法的瓶颈就在于第二步的操作，最简单且最快的方法是用并查集。我们都知道并查集是一个非常快速的数据结构，查询为O(1)O(1)，算上这一步的枚举，整个第二步的时间复杂度就是O(m)O(m)，判断两点是否连通和加入到集合中就是并查集的基本操作

虽然思路十分简单，但是我们还是需要注意几点：

  • ①Kruskal算法在数据量大的情况下（如N<=1e5）是比Prim算法优很多的，因此在解决最小生成树问题的时候我们基本上都选择Krusual算法
  • ②Kruskal算法不需要用邻接表或者邻接矩阵来存图，只需要开一个结构体来存储边就可以了，相比于Prim算法节省很多空间（1e5在邻接表里面已经爆掉了）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5+10;

int n,m;
int p[N];

struct Edge
{
    int a,b,w;
    //重载一下小于号
    bool operator < (const Edge &W)const
    {
        return w<W.w;
    }
}edges[N];
//并查集，找一个点属于的集合
int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    cin >> n >> m;
    //存边
    for(int i=0;i<m;i++)
    {
        int a,b,w;
        cin >> a >> b >> w;
        edges[i] = {a,b,w};
    }
    //排序
    sort(edges,edges+m);
    //初始化并查集
    for(int i=1;i<=n;i++) p[i] = i;
    //res为权值和，cnt为边的数量
    int res = 0,cnt = 0;
    for(int i=0;i<=m;i++)
    {
        int a = edges[i].a,b = edges[i].b,w = edges[i].w;
        a = find(a),b = find(b);
        //不连通，让他们连通
        if(a!=b)
        {
            p[a] = b;
            res+=w;
            cnt++;
        }
    }
    //边数小于n-1，不是最小生成树
    if(cnt<n-1) cout << "impossible";
    else cout << res;
    return 0;
}