KMP

题目链接：Acwing 831. KMP字符串

KMP的过程一般比较抽象，较难理解。

  • 题目背景：
1
2
3
给定一个字符串S，以及一个模式串P，所有字符串中只包含大小写英文字母以及阿拉伯数字。
模式串P在字符串S中多次作为子串出现。
求出模式串P在字符串S中所有出现位置的起始下标。

我们先考虑暴力算法怎么做，然后怎么去优化：

  • 假如s是比较长的串，p是比较短的串，我们可以遍历s的同时遍历p，即写一个二重循环。这么做的目的是为了按位匹配。在这个过程中设置一个变量flag来记录是否成功匹配。
  • 假如出现不匹配的情况，即s[i+j-1]!=p[i]，那么我们直接break，同时把flag变为false

这个时间复杂度是感人的，为O(n∗m)O(n*m )，对于10510^{5}以上的数据量就不适用了。为了方便演示，我用表格来模拟一下其过程：


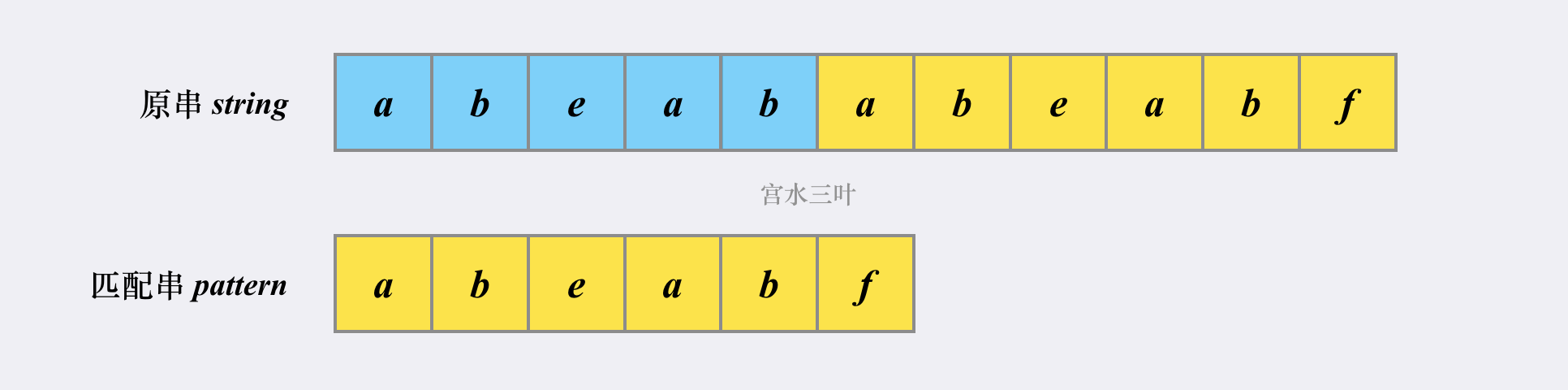
对于常规解法，我们会对两个字符串进行遍历，最后得到以下的结果：

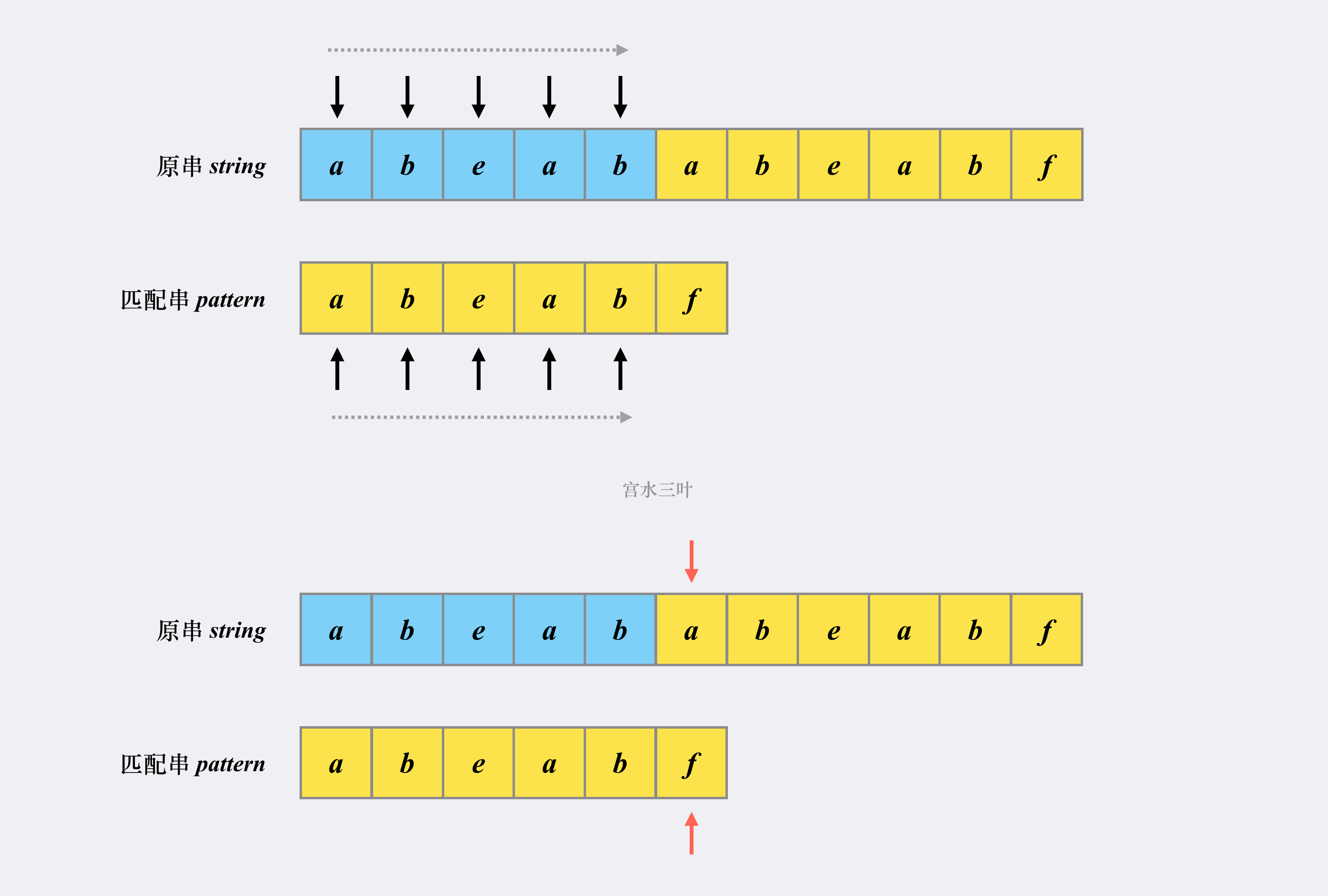
那我们发现失配了，怎么办呢？只能重头开始遍历：

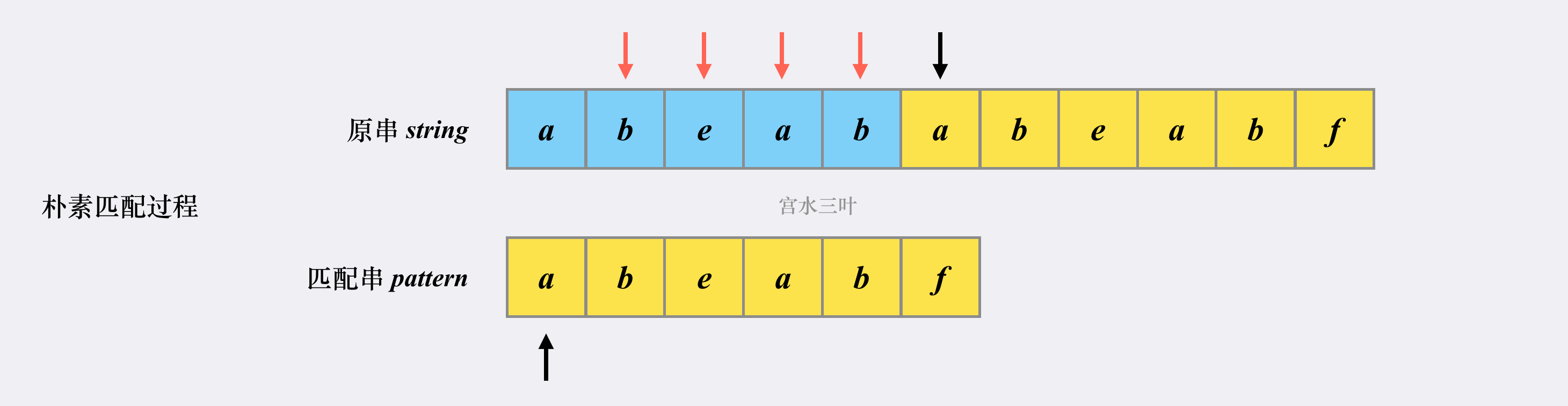
因此时间复杂度为O(n∗m)O(n*m)，这是因为最坏情况下我们需要遍历所有的子串。

那么KMP算法是怎么样的呢？KMP算法和朴素解法一样，也是先遍历两个字符串，也就是两重循环不变。那么优化之处就在于失配后不重头开始遍历

怎么优化呢？我们可以把匹配过程看成模式串的平移（也就是指针的移动），我们需要找到一个最简单的平移，使得平移后的模式串失配位置前的部分和原串失配位置前的部分相匹配

这段文字比较抽象，我们还是拿上面的图来举例子：

对于匹配串，我们在5号位置失配了，我们要尽可能少的平移，为了满足上面的规则，我们把其平移成如下形式：

1
2
a b e a b a b e a b f
      a b e a b f

我们可以发现：我们模式串的前缀刚好和原串失配位置前的后缀是相同的，此时我们的平移最优

我们把匹配失败的模式串搞回来：

1
2
3
原串：  a b e a b a b e a b f
失配：  a b e a b f
平移：        a b e a b f

我们发现，就我们讨论的部分，即平移后的前缀，和失配时的后缀是相同的，说明我们的平移位置与原串无关，只与模式串本身有关
这点十分重要，是整个KMP算法的核心：

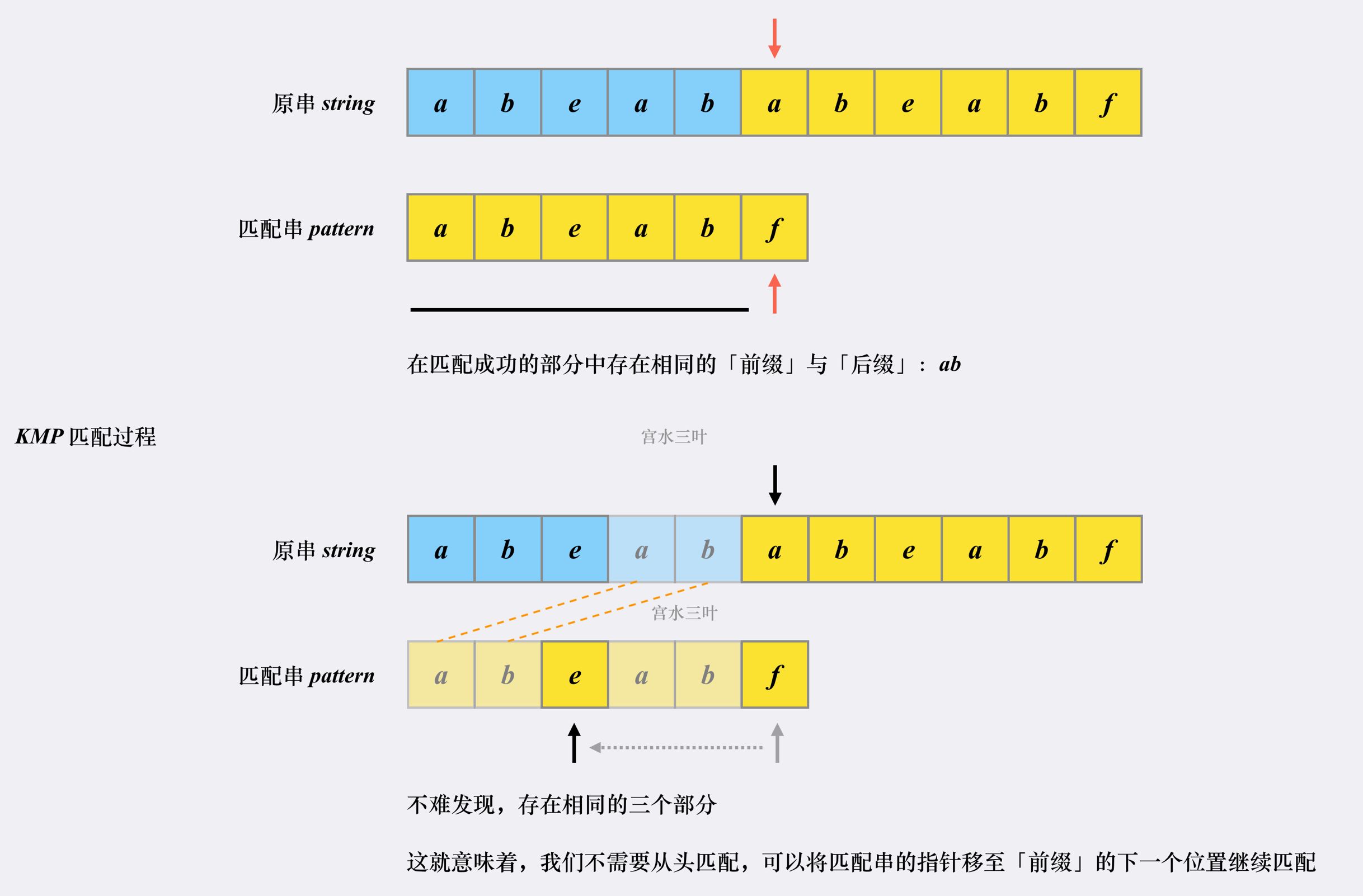
接下来算法的重点，无非就是根据模式串算出我们的平移位置

next点

计算的过程，我们称之为寻找next点，本质上就是寻找模式串长度相同的前缀和后缀的最大长度。

我们用next[i]表示模式串下标为i的点在平移后的下标

我们还是拿出上面的例子，不同的是，这里我们标上下标

1
2
3
4
5
6
原串：  a b e a b   a b e a b  f
下标：          i-1 i
失配：  a b e a b f
下标：          j j+1
平移：        a b e a b f
下标：     next[j]

根据next数组的定义，b的下标为j，平移后对应的下标应该是next[j]，这是十分显然的。因此我们的j可以直接改为next[j]，直到我们的j = 0（退无可退了，也就是必须要重新开始匹配），或者s[i] == p[j+1]（也就是我们下一位可以匹配，不满足我们寻找next点的条件），此时我们停止更新。假如满足后者，我们就可以直接进行下一位了，即j++，随后更新我们的next[i] = j

具体代码如下：

1
2
3
4
5
6
7
8
9
for(int i=2,j=0;i<=n;i++)
{
      //如果失配，跳到next[i]，直到退无可退了
      while(j && p[i]!=p[j+1]) j = ne[j];
      //如果可配，就j右移
      if(p[i] == p[j+1]) j++;
      //更新next
      ne[i] = j;
}

最关键的一步解决了，整个题目就解决了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <bits/stdc++.h>
using namespace std;
const int N = 100100,M = 1000100;

int n,m;
char p[N],s[M];
int ne[N];

int main()
{
    cin >> n >> p+1 >> m >> s+1;

    for(int i=2,j=0;i<=n;i++)
    {
        //如果失配，跳到next[i]，直到退无可退了
        while(j && p[i]!=p[j+1]) j = ne[j];
        //如果可配，就j右移
        if(p[i] == p[j+1]) j++;
        //更新next
        ne[i] = j;
    }

    for(int i=1,j=0;i<=m;i++)
    {
        //如果j不能往前走，就往前退到next[j]，看看是不是能继续走
        //如果j退无可退，那么就下一次循环了
        while(j && s[i]!=p[j+1]) j = ne[j];
        //如果一样，那么就可以往后走
        if(s[i] == p[j+1]) j++;
        //匹配成功
        if(j == n)
        {
            //输出下标差
            cout << i-n << " ";
            //回退
            j = ne[j];
        }
    }
    return 0;
}